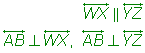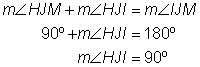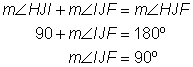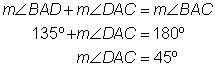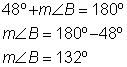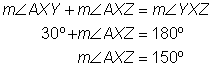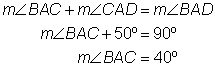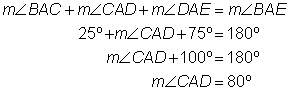Reading: Properties of Angles
Learning Objective(s)
·Identify parallel and perpendicular lines.
·Find measures of angles.
·Identify complementary and supplementary angles.
Introduction
Imagine two separate and distinct lines on a plane. There are two possibilities for these lines: they will either intersect at one point, or they will never intersect. When two lines intersect, four angles are formed. Understanding how these angles relate to each other can help you figure out how to measure them, even if you only have information about the size of one angle.
Parallel lines are two or more lines that never intersect. Likewise, parallel line segments are two line segments that never intersect even if the line segments were turned into lines that continued forever. Examples of parallel line segments are all around you, in the two sides of this page and in the shelves of a bookcase. When you see lines or structures that seem to run in the same direction, never cross one another, and are always the same distance apart, there's a good chance that they are parallel.
Perpendicular lines are two lines that intersect at a 90º (right) angle. And perpendicular line segments also intersect at a 90º (right) angle. You can see examples of perpendicular lines everywhere as well--on graph paper, in the crossing pattern of roads at an intersection, to the colored lines of a plaid shirt. In our daily lives, you may be happy to call two lines perpendicular if they merely seem to be at right angles to one another. When studying geometry, however, you need to make sure that two lines intersect at a 90º angle before declaring them to be perpendicular.
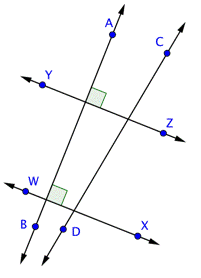
The image below shows some parallel and perpendicular lines. The geometric symbol for parallel is ![]() , so you can show that
, so you can show that ![]() . Parallel lines are also often indicated by the marking >> on each line (or just a single > on each line). Perpendicular lines are indicated by the symbol
. Parallel lines are also often indicated by the marking >> on each line (or just a single > on each line). Perpendicular lines are indicated by the symbol ![]() , so you can write
, so you can write ![]() .
.
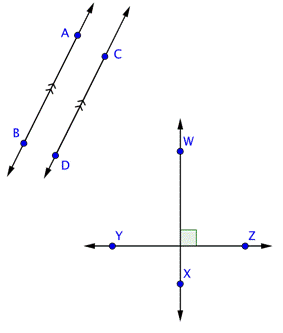
If two lines are parallel, then any line that is perpendicular to one line will also be perpendicular to the other line. Similarly, if two lines are both perpendicular to the same line, then those two lines are parallel to each other. Let's take a look at one example and identify some of these types of lines.
Example | ||
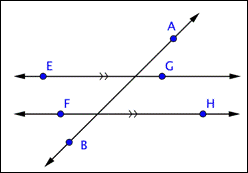
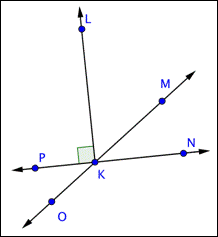
Problem | Identify a set of parallel lines and a set of perpendicular lines in the image below.
| |
| Parallel lines never meet, and perpendicular lines intersect at a right angle.
| |
|
| |
| Since | |
Answer |
| |
Which statement most accurately represents the image below?
A) B) C) D) |
Understanding how parallel and perpendicular lines relate can help you figure out the measurements of some unknown angles. To start, all you need to remember is that perpendicular lines intersect at a 90º angle, and that a straight angle measures 180º.
The measure of an angle such as ![]() is written as
is written as ![]() . Look at the example below. How can you find the measurements of the unmarked angles?
. Look at the example below. How can you find the measurements of the unmarked angles?
Example | ||
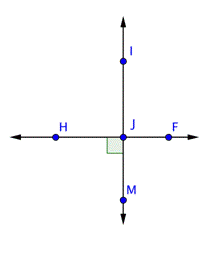
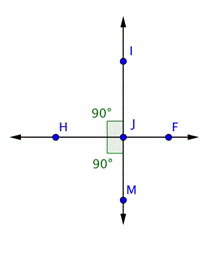
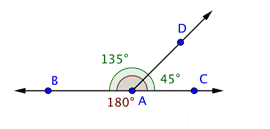
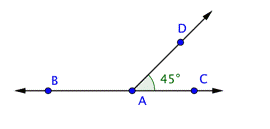
Problem | Find the measurement of
| |
| Only one angle,
| |
| You can use this information to find the measurement of
| |
| Now use the same logic to find the measurement of
| |
| You know that measures 90º. Use this information to find the measurement of
| |
Answer |
| |
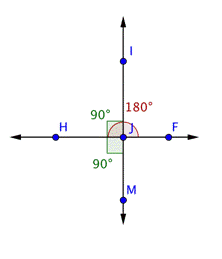
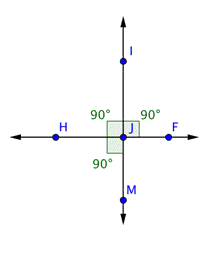
In this example, you may have noticed that angles ![]() , and
, and ![]() are all right angles. (If you were asked to find the measurement of
are all right angles. (If you were asked to find the measurement of ![]() , you would find that angle to be 90º, too.) This is what happens when two lines are perpendicular--the four angles created by the intersection are all right angles.
, you would find that angle to be 90º, too.) This is what happens when two lines are perpendicular--the four angles created by the intersection are all right angles.
Not all intersections happen at right angles, though. In the example below, notice how you can use the same technique as shown above (using straight angles) to find the measurement of a missing angle.
Example | ||
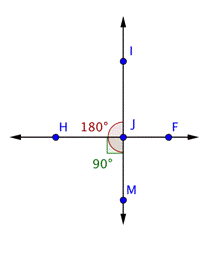
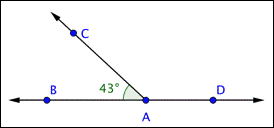
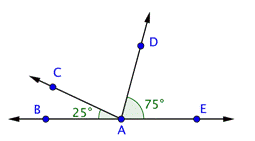
Problem | Find the measurement of
| |
| This image shows the line | |
|
| |
| Use this information to find the measurement of
| |
Answer |
| |
Find the measurement of
A) 43º B) 137º C) 147º D) 317º |
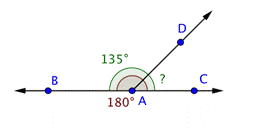
In the example above, ![]() and
and ![]() add up to 180º. Two angles whose measures add up to 180º are called supplementary angles. There's also a term for two angles whose measurements add up to 90º, they are called complementary angles.
add up to 180º. Two angles whose measures add up to 180º are called supplementary angles. There's also a term for two angles whose measurements add up to 90º, they are called complementary angles.
One way to remember the difference between the two terms is that "corner” and "complementary” each begin with c (a 90º angle looks like a corner), while straight and "supplementary” each begin with s (a straight angle measures 180º).
If you can identify supplementary or complementary angles within a problem, finding missing angle measurements is often simply a matter of adding or subtracting.
Example | ||
Problem | Two angles are supplementary. If one of the angles measures 48º, what is the measurement of the other angle? | |
| Two supplementary angles make up a straight angle, so the measurements of the two angles will be 180º. | |
| You know the measurement of one angle. To find the measurement of the second angle, subtract 48º from 180º. | |
Answer | The measurement of the other angle is 132º. | |
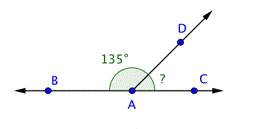
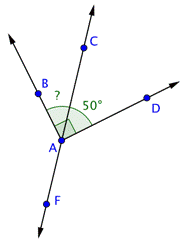
Example | ||
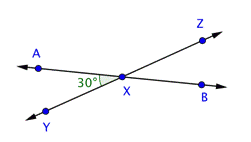
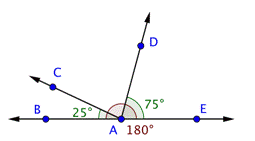
Problem | Find the measurement of
| |
| This image shows two intersecting lines, Angles | |
| Use this information to find the measurement of
| |
Answer |
| |
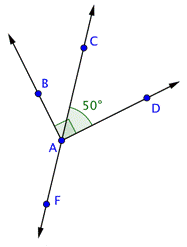
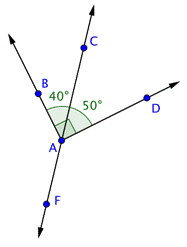
Example | ||
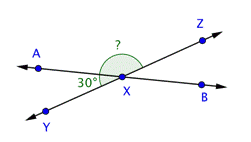
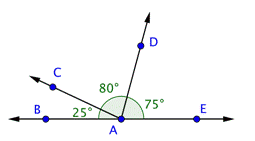
Problem | Find the measurement of
| |
| This image shows the line Angles | |
| Use this information to find the measurement of
| |
Answer |
| |
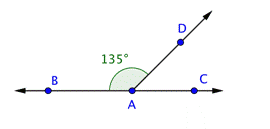
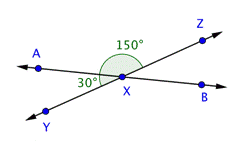
Example | ||
Problem | Find the measurement of
| |
| You know the measurements of two angles here: | |
| Use this information to find the measurement of
| |
Answer |
| |
Which pair of angles is complementary?
A) B) C) D) |
Summary
Parallel lines do not intersect, while perpendicular lines cross at a 90º angle. Two angles whose measurements add up to 180º are said to be supplementary, and two angles whose measurements add up to 90º are said to be complementary. For most pairs of intersecting lines, all you need is the measurement of one angle to find the measurements of all other angles formed by the intersection.
Permissions
This reading is taken from the Developmental Math Open Program created by The NROC Project. It is available under a Creative Commons license.