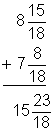Reading: Adding Fractions
Learning Objectives
·Add fractions with like denominators.
·Find the least common multiple (LCM) of two or more numbers.
·Find the common denominator of fractions with unlike denominators.
·Add fractions with unlike denominators.
·Add mixed numbers with like and unlike denominators.
·Solve application problems that require the addition of fractions or mixed numbers.
Introduction
Fractions are used in many areas of everyday life: recipes, woodworking, rainfall, timecards, and measurements, to name just a few. Sometimes you have parts of wholes that you need to combine. Just as you can add whole numbers, you can add fractions and mixed numbers. Consider, for example, how to determine the monthly rainfall if you know the daily rainfall in inches. You have to add fractions. Also, consider several painters who are working to paint a house together with multiple cans of paint. They might add the fractions of what remains in each can to determine if there is enough paint to finish the job or if they need to buy more.
When the pieces are the same size, they can easily be added. Consider the pictures below showing the fractions ![]() and
and ![]() .
.
This picture represents ![]() shaded because 3 out of 6 blocks are shaded.
shaded because 3 out of 6 blocks are shaded.
|
|
|
|
|
|
This picture represents ![]() shaded because 2 out of 6 blocks are shaded.
shaded because 2 out of 6 blocks are shaded.
If you add these shaded blocks together, you are adding ![]() +
+ ![]() .
.
You can create a new picture showing 5 shaded blocks in a rectangle containing 6 blocks.
So, ![]() .
.
Without drawing rectangles and shading boxes, you can get this answer simply by adding the numerators, 3 + 2, and keeping the denominator, 6, the same. This procedure works for adding any fractions that have the same denominator, called like denominators.
Example | |||
Problem |
| Add. | |
| Since the denominator of each fraction is 5, these fractions have like denominators. So, add the numerators and write the sum over the denominator, 5. | ||
Answer |
| ||
Example | |||
Problem |
| Add. Simplify the answer. | |
= | The denominators are alike, so add the numerators. | ||
| Simplify the fraction. | ||
Answer |
| ||
Example | |||
Problem |
| Add. Simplify the answer and write as a mixed number. | |
= | The denominators are alike, so add the numerators. | ||
| Simplify the fraction. 16 and 12 have a common factor of 4. | ||
| Write the improper fraction as a mixed number, by dividing: 4 ÷ 3 = 1 with a remainder of 1. | ||
Answer |
| ||
In the previous example, the fraction was simplified and then converted to a mixed number. You could just as easily have first converted the improper fraction to a mixed number and then simplified the fraction in the mixed number. Notice that the same answer is reached with both methods.
![]() =
= ![]()
The fraction ![]() can be simplified.
can be simplified. ![]()
But, don't forget about the 1 that is part of the mixed number! The final answer is ![]() .
.
Adding Fractions with Like Denominators 1.Add the numerators (the number in the top of each fraction). 2.Keep the denominator (the bottom number) the same. 3.Simplify to lowest terms. |
A) B) C) D) |
Sometimes fractions do not have the same denominator. They have unlike denominators. Think about the example of the house painters. If one painter has ![]() can of paint and his painting partner has
can of paint and his painting partner has ![]() can of paint, how much do they have in total? How can you add these fractions when they do not have like denominators?
can of paint, how much do they have in total? How can you add these fractions when they do not have like denominators?
The answer is that you can rewrite one or both of the fractions so that they have the same denominator. This is called finding a common denominator. While any common denominator will do, it is helpful to find the least common multiple of the two numbers in the denominator because this will save having to simplify at the end. The least common multiple is the least number that is a multiple of two or more numbers. Least common multiple is sometimes abbreviated LCM.
There are several ways to find common multiples, some of which you used when comparing fractions. To find the least common multiple (LCM), you can list the multiples of each number and determine which multiples they have in common. The least of these numbers will be the least common multiple. Consider the numbers 4 and 6. Some of their multiples are shown below. You can see that they have several common multiples, and the least of these is 12.
4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 | 44 | 48 | 52 | 56 | 60 | 64 | |
6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 | 66 | 68 |
Example | |||||
Problem | Find the least common multiple of 30 and 50. | ||||
30, 60, 90, 120, 150,180, 210, 240 | List some multiples of 30. | ||||
50, 100, 150, 200, 250 | List some multiples of 50. | ||||
150 is found on both lists of multiples. | Look for the least number found on both lists. | ||||
Answer | The least common multiple of 30 and 50 is 150. | ||||
The other method for finding the least common multiple is to use prime factorization. This is the method you need for working with rational expressions. The following shows how the factor method works with the numeric example, 4 and 6.
Start by finding the prime factorization of each denominator:
4 | = | 2 | • | 2 |
6 | = | 3 | • | 2 |
Identify the greatest number of times any factor appears in either factorization and multiply those factors to get the least common multiple. For 4 and 6, it would be:
3 • 2 • 2 = 12
Notice that 2 is included twice, because it appears twice in the prime factorization of 4. 12 is the least common multiple of 4 and 6.
The next example also shows how to use prime factorization.
Example | ||||||
Problem | Find the least common multiple of 28 and 40. | |||||
28 = 2 • 2 • 7 | Write the prime factorization of 28. | |||||
40= 2 • 2 • 2 • 5 | Write the prime factorization of 40. | |||||
2 • 2 • 2 • 5 • 7= 280 | Write the factors the greatest number of times they appear in either factorization and multiply. | |||||
Answer | The least common multiple of 28 and 40 is 280. | |||||
Find the least common multiple of 12 and 80. A) 240 B) 120 C)960 D) 480 |
You can use the least common multiple of two denominators as the least common denominator for those fractions. Then you rewrite each fraction using the same denominator.
The example below shows how to use the least common multiple as the least common denominator.
Example | |||||||
Problem | Rewrite the fractions | ||||||
Multiples of 3: 3, 6, 9, 12 Multiples of 2: 2, 4, 6 6 is the least common denominator. | Find the least common multiple of the denominators. This is the least common denominator. | ||||||
| Rewrite | ||||||
| Rewrite | ||||||
Answer | The fraction The fraction | ||||||
Find the least common denominator. Then express each fraction using the least common denominator:
A) B) C) 24 D) |
To add fractions with unlike denominators, first rewrite them with like denominators. Then, you know what to do! The steps are shown below.
Adding Fractions with Unlike Denominators 1.Find a common denominator. 2.Rewrite each fraction using the common denominator. 3.Now that the fractions have a common denominator, you can add the numerators. 4.Simplify to lowest terms, expressing improper fractions as mixed numbers. |
You can always find a common denominator by multiplying the two denominators together. See the example below.
Example | |||
Problem |
| Add. Simplify the answer. | |
3 • 5 = 15 | Since the denominators are not alike, find a common denominator by multiplying the denominators. | ||
| Rewrite each fraction with a denominator of 15. | ||
| Add the fractions by adding the numerators and keeping the denominator the same. Make sure the fraction cannot be simplified. | ||
Answer |
| ||
You can find a common denominator by finding the common multiples of the denominators. The least common multiple is the easiest to use.
Example | |||||
Problem |
| Add. Simplify the answer. | |||
Multiples of 7: 7, 14, 21 Multiples of 21: 21 | Since the denominators are not alike, find the least common denominator by finding the least common multiple (LCM) of 7 and 21. | ||||
| Rewrite each fraction with a denominator of 21. | ||||
| Add the fractions by adding the numerators and keeping the denominator the same. Make sure the fraction cannot be simplified. | ||||
Answer |
| ||||
You can also add more than two fractions as long as you first find a common denominator for all of them. An example of a sum of three fractions is shown below. In this example, you will use the prime factorization method to find the LCM.
Example | |||||
Problem |
| Add. Simplify the answer and write as a mixed number. | |||
4 = 2 • 2 6 = 3 • 2 8 = 2 • 2 • 2 LCM: 2 • 2 • 2 • 3 = 24 | Since the denominators are not alike, find the least common denominator by finding the least common multiple (LCM) of 4, 6 and 8. | ||||
| Rewrite each fraction with a denominator of 24. | ||||
| Add the fractions by adding the numerators and keeping the denominator the same. | ||||
| Write the improper fraction as a mixed number and simplify the fraction. | ||||
Answer |
| ||||
A) B) C) D) |
Just as you can add whole numbers and proper fractions, you can also add mixed numbers. To add mixed numbers, add the whole numbers together and the fraction parts of the mixed numbers together and then recombine to express the value as a mixed number. The steps for adding two mixed numbers are shown in the examples below.
You can keep the whole numbers and the fractions together using a vertical method for adding mixed numbers as shown below.
Example | ||||
Problem |
| Add. Simplify the answer and write as a mixed number. | ||
| Arrange the mixed numbers vertically so the whole numbers align and the fractions align. | |||
| Add whole numbers. Add fractions. | |||
| Simplify the fraction. | |||
Answer |
| |||
When adding mixed numbers you may also need to find a common denominator first. Consider the example below.
Example | ||||
Problem |
| Add. Simplify the answer andwrite as a mixed number. | ||
Multiples of 6: 6, 12, 18 Multiple of 9: 9, 18 | Find a least common denominator for the fractions. | |||
| Express each fraction with a denominator of 18. | |||
| Arrange the mixed numbers vertically so the whole numbers align and the fractions align. | |||
| Add whole numbers. Add fractions. | |||
| Write the improper fraction as a mixed number. | |||
15 + 1+
| Combine whole numbers and fraction to write a mixed number. | |||
Answer |
| |||
A) B) C) D) |
Knowing how to add fractions is useful in a variety of situations. When reading problems, look for phrases that help you know you want to add the fractions.
Example | |||||
Problem | A stack of pamphlets is placed on top of a book. If the stack of pamphlets is | ||||
| Find the total height of the pile by adding the thicknesses of the stack of pamphlets and the book. | ||||
| Group the whole numbers and fractions to make adding easier. | ||||
| Add whole numbers. | ||||
8+ 1 = 9 | Add fractions. Combine whole number and fraction. | ||||
Answer | The pile is 9 inches high. | ||||
Example | |||||
Problem | A cake recipe requires | ||||
| Find the total amount of liquid by adding the quantities. | ||||
| Group the whole numbers and fractions to make adding easier. | ||||
| Add whole numbers. | ||||
| Add fractions. Recall that Combine whole number and fraction. | ||||
Answer | There are | ||||
What is the total rainfall in a three-day period if it rains A) 6 inches B) C) D) |
Summary
Adding fractions with like denominators involves adding the numerators and keeping the denominator the same. Always simplify the answer. To add fractions with unlike denominators, first find a common denominator. The least common denominator is easiest to use. The least common multiple can be used as the least common denominator. Adding mixed numbers involves adding the fractional parts, adding the whole numbers, and then recombining them as a mixed number.
Permissions
This reading is taken from the Developmental Math Open Program created by The NROC Project. It is available under a Creative Commons license.