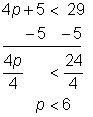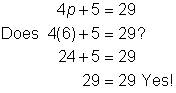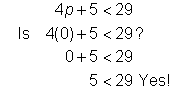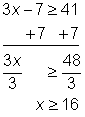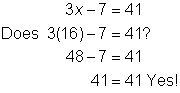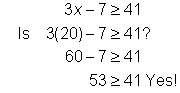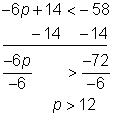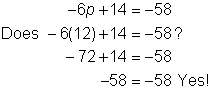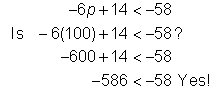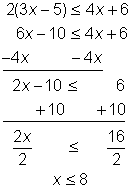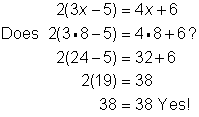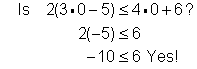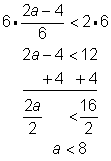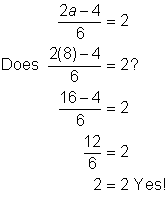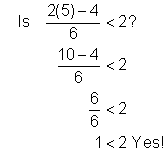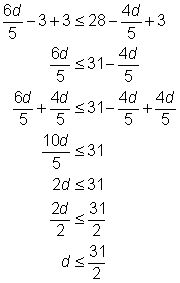Reading: Multi-Step Inequalities
Learning Objective(s)
·Use the properties of inequality together to isolate variables and solve algebraic inequalities, and express their solutions graphically.
·Simplify and solve algebraic inequalities using the distributive property to clear parentheses and fractions.
Introduction
Solving multi-step inequalities is very similar to solving equations--what you do to one side you need to do to the other side in order to maintain the "balance” of the inequality. The Properties of Inequality can help you understand how to add, subtract, multiply, or divide within an inequality.
A popular strategy for solving equations, isolating the variable, also applies to solving inequalities. By adding, subtracting, multiplying and/or dividing, you can rewrite the inequality so that the variable is on one side and everything else is on the other. As with one step inequalities, the solutions to multi-step inequalities can be graphed on a number line.
Example | ||||
Problem | Solve for p. 4p + 5 < 29 | |||
| Begin to isolate the variable by subtracting 5 from both sides of the inequality. Divide both sides of the inequality by 4 to express the variable with a coefficient of 1. | |||
Answer |
| |||
To graph this inequality, you draw an open circle at the end point 6 on the number line. The circle is open because the inequality is less than 6 and not equal to 6. The values where p is less than 6 are found all along the number line to the left of 6. Draw a blue line with an arrow on the number line pointing in that direction.
To check the solution, substitute the end point 6 into the original inequality written as an equation, which is called the related equation, to see if you get a true statement. Then check another solution, such as 0, to see if the inequality is correct.
Example | |||
Problem | Check that p < 6 is the solution to the inequality 4p + 5 < 29. | ||
| Check the end point 6 in the related equation. | ||
| Try another value to check the inequality. Let's use p = 0. | ||
Answer p < 6 is the solution to the inequality 4p + 5 < 29. | |||
Example | |||||
Problem | Solve for x. 3x - 7 ≥ 41 | ||||
| Begin to isolate the variable by adding 7 to both sides of the inequality. Divide both sides of the inequality by 3 to express the variable with a coefficient of 1. | ||||
Check |
| First, check the end point 16 in the related equation. Then, try another value to check the inequality. Let's use x = 20. | |||
Answer |
| ||||
When solving multi-step equations, pay attention to situations in which you multiply or divide by a negative number. In these cases, you must reverse the inequality sign.
Example | |||||
Problem | Solve for p. −6p + 14 < −58 | ||||
| Begin to isolate the variable by subtracting 14 from both sides of the inequality. Divide both sides of the inequality by −6 to express the variable with a coefficient of 1. Dividing by a negative number results in reversing the inequality sign. | ||||
Check |
| Check the solution. First, check the end point 12 in the related equation. Then, try another value to check the inequality. Try 100. | |||
Answer |
| ||||
The graph of the inequality p > 12 has an open circle at 12 with an arrow stretching to the right.
Advanced Example | |||||
Problem | Solve for x.
| ||||
| To isolate the variable, subtract Then multiply by 3 so that the coefficient in front of the parentheses is 1. Then subtract 3 from both sides. | ||||
Check |
| Check the solution. First, check the end point -18 in the related equation. | |||
| Now check any value for x that is within the region The statement is true. | ||||
Answer |
| ||||
from both sides of the inequality.
. We will use 
.Advanced Question A student is solving the inequality A) B) C) D) |
. If she combines like terms, which of the following inequalities could she see?
As with equations, the distributive property can be applied to simplify expressions that are part of an inequality. Once the parentheses have been cleared, solving the inequality will be straightforward.
Example | |||||
Problem | Solve for x. 2(3x - 5) ≤ 4x + 6 | ||||
| Distribute to clear the parentheses. Subtract 4x from both sides to get the variable term on one side only. Add 10 to both sides to isolate the variable. Divide both sides by 2 to express the variable with a coefficient of 1. | ||||
Check |
| Check the solution. First, check the end point 8 in the related equation. Then, choose another solution and evaluate the inequality for that value to make sure it is a true statement. Try 0. | |||
Answer |
| ||||
Example | ||||
Problem | Solve for a.
| |||
| Clear the fraction by multiplying both sides of the equation by 6. Add 4 to both sides to isolate the variable. Divide both sides by 2 to express the variable with a coefficient of 1. | |||
Check |
| Check the solution. First, check the end point 8 in the related equation. Then, choose another solution and evaluate the inequality for that value to make sure it is a true statement. Try 5. | ||
Answer |
| |||
Advanced Example | |||||
Problem | Solve for d.
| ||||
| This inequality contains two parentheses. Use the Distributive Property to expand both sides of the inequality. | ||||
| Now that both sides have been expanded, combine like terms and find the range of values for d. | ||||
Check |
| Check the solution. First, check the end point It results in a true statement. | |||
| Now try any value for d that is within the region This is also a true statement. | ||||
Answer | | ||||
in the related equation.
. We will try 
Which is the most logical first step for solving for the variable in the inequality: 8x + 7 < 3(2x + 1) A) Reverse the inequality sign. B) Use the distributive property to clear the parentheses by multiplying each of the terms in the parentheses by 3. C) Subtract 2x from both sides of the inequality. D) Divide both sides of the inequality by 3. |
Advanced Question Solve for x. A) B) C) D) |
Summary
Inequalities can have a range of answers. The solutions are often graphed on a number line in order to visualize all of the solutions. Multi-step inequalities are solved using the same processes that work for solving equations with one exception. When you multiply or divide both sides of an inequality by a negative number, you must reverse the inequality symbol. The inequality symbols stay the same whenever you add or subtract either positive or negative numbers to both sides of the inequality.
Permissions
This reading is taken from the Developmental Math Open Program created by The NROC Project. It is available under a Creative Commons license.
Última modificación: jueves, 25 de agosto de 2016, 09:22