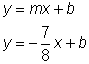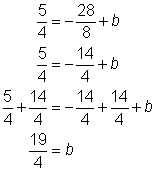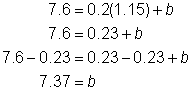Reading: Writing the Equation of a Line
Learning Objective(s)
·Find the slope and the y-intercept, and write an equation of the line.
·Given the slope and a point on the line, write an equation of the line.
·Given two points, write the equation of a line.
Introduction
A linear equation can be expressed in the form![]() . In this equation, x and y are coordinates of a point, m is the slope, and b is they-coordinate of the y-intercept. Because this equation describes a line in terms of its slope and its y-intercept, this equation is called theslope-intercept form. When working with linear relationships, the slope-intercept form helps to translate between the graph of a line and the equation of a line.
. In this equation, x and y are coordinates of a point, m is the slope, and b is they-coordinate of the y-intercept. Because this equation describes a line in terms of its slope and its y-intercept, this equation is called theslope-intercept form. When working with linear relationships, the slope-intercept form helps to translate between the graph of a line and the equation of a line.
Simply by changing the values of m and b, you can define any line. That's how powerful and versatile the slope-intercept formula is.
Now that you understand the slope-intercept form, you can look at the graph of a line and write its equation just by identifying the slope and the y-intercept from the graph. Let's try it with this line.
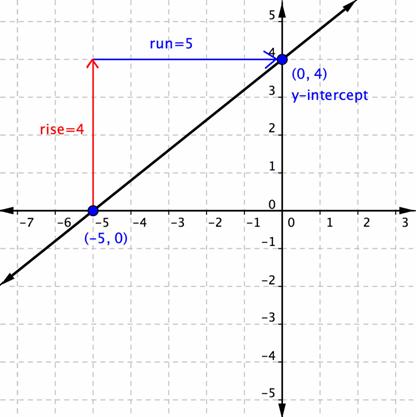
For this line, the slope is ![]() , and the y-intercept is 4. If you put those values into the slope-intercept form, y = mx + b, you get the equation
, and the y-intercept is 4. If you put those values into the slope-intercept form, y = mx + b, you get the equation ![]() .
.
Example | ||
Problem | Write the equation of the line that has a slope of | |
| Substitute the slope (m) into y = mx + b. | |
Answer |
or
| Substitute the y-intercept (b) into the equation. |
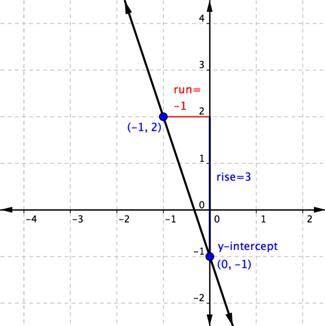
If you know the slope of a line and a point on the line, you can draw a graph. So using an equation in the point-slope form, you can easily identify the slope and a point. Consider the equation ![]() . You can tell from this equation that the y-intercept is at (0, −1). Start by plotting that point, (0, −1), on a graph.
. You can tell from this equation that the y-intercept is at (0, −1). Start by plotting that point, (0, −1), on a graph.
You can also tell from the equation that the slope of this line is −3. So start at (0, −1) and count up 3 and over −1 (1 unit in the negative direction, left) and plot a second point. (You could also have gone down 3 and over 1.) Then draw a line through both points, and there it is, the graph of ![]() .
.
What is the equation of a line that has a slope of −2 and goes through the point (0, 8)? A) y = −2x + 8 B) y = 8x - 2 C) y = −2x + 0 D) 0 = 8x - 2 |
Using slope-intercept form to help write the equation of a line is possible when you know both the slope (m) and the y-intercept (b), but what if you know the slope and just any point on the line, not specifically the y-intercept? Can you still write the equation? The answer is yes, but you will need to put in a little more thought and work than you did previously.
Recall that a point is an (x, y) coordinate pair and that all points on the line will satisfy the linear equation. So, if you have a point on the line, it must be a solution to the equation. Although you don't know the exact equation yet, you know that you can express the line in slope-intercept form, y = mx + b.
You do know the slope (m), but you just don't know the value of the y-intercept (b). Since point (x, y) is a solution to the equation, you can substitute its coordinates for x and y in y = mx + b and solve to find b!
This may seem a bit confusing with all the variables, but an example with an actual slope and a point will help to clarify.
Example | ||
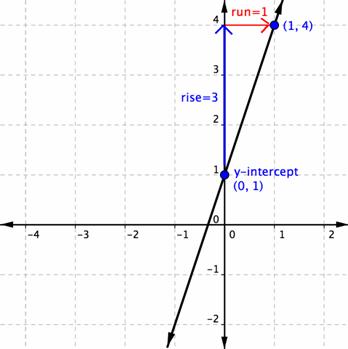
Problem | Write the equation of the line that has a slope of 3 and contains the point (1, 4). | |
y = 3x + b | Substitute the slope (m) into y = mx + b. | |
4 = 3(1) + b | Substitute the point (1, 4) for x and y. | |
4 = 3 + b 1 = b | Solve for b. | |
Answer | y = 3x + 1 | Rewrite y = mx + b withm = 3 and b = 1. |
To confirm our algebra, you can check by graphing the equation y = 3x + 1. The equation checks because when graphed it passes through the point (1, 4).
Advanced Example | ||
Problem | Write the equation of the line that has a slope of | |
| Substitute the slope (m) into | |
| Substitute the point | |
| Solve for b. | |
Answer |
| Rewrite |
Write the slope-intercept form of the line with a slope of point (9, 4). A) B) C) D) |
Advanced Question Write the slope-intercept form of the line with a slope of -0.6 and which contains the point (3.8, 7.25). A) y = -0.6x + 3.8 B) y = -0.6x + 4.97 C) y = 3.8x + 7.25 D) y = -0.6x + 9.53 |
Let's suppose you don't know either the slope or the y-intercept, but you do know the location of two points on the line. It is more challenging, but you can find the equation of the line that would pass through those two points. You will again use slope-intercept form to help you.
The slope of a linear equation is always the same, no matter which two points you use to find the slope. Since you have two points, you can use those points to find the slope (m). Now you have the slope and a point on the line! You can now substitute values for m, x, and y into the equation y = mx + b and find b.
Example | ||
Problem | Write the equation of the line that passes through the points (2, 1) and (−1, −5). | |
| Find the slope using the given points. | |
y = 2x + b | Substitute the slope (m) into y = mx + b. | |
1 = 2(2) + b | Substitute the coordinates of either point for x and y- this example uses (2, 1). | |
1 = 4 + b −3 = b | Solve for b. | |
Answer | y = 2x + (−3), or y = 2x - 3 | Rewrite y = mx + b withm = 2 and b = −3. |
Notice that is doesn't matter which point you use when you substitute and solve for b--you get the same result for b either way. In the example above, you substituted the coordinates of the point (2, 1) in the equation y = 2x + b. Let's start with the same equation, y = 2x + b, but substitute in (−1, −5):
y = 2x + b |
−5 = 2(−1) + b |
−5 = −2 + b |
−3 = b |
The final equation is the same: y = 2x - 3.
Advanced Example | ||
Problem | Write the equation of the line that passes through the points (-4.6,6.45) and (1.15,7.6). | |
| Find the slope using the given points. | |
| Substitute the slope (m) into | |
| Substitute either point for x and y- this example uses (1.15,7.6). Then solve for b. | |
| Rewrite | |
Answer | The equation of the line that passes through the points (-4.6,6.45) and (1.15,7.6) is | |
Write the slope-intercept form of the line that passes through (5, 2) and (−1, −10). A) B) C) D) |
Advanced Question Which of the following lines goes through the points A) B) C) D) |
Summary
The slope-intercept form of a linear equation is written as y = mx + b, where m is the slope and b is the value of y at the y-intercept, which can be written as (0, b). When you know the slope and the y-intercept of a line you can use the slope-intercept form to immediately write the equation of that line. The slope-intercept form can also help you to write the equation of a line when you know the slope and a point on the line or when you know two points on the line.
Permissions
This reading is taken from the Developmental Math Open Program created by The NROC Project. It is available under a Creative Commons license.