Reading: Adding and Subtracting Polynomials
Learning Objectives
·Add polynomials.
·Find the opposite of a polynomial.
·Subtract polynomials.
Introduction
Adding and subtracting polynomials may sound complicated, but it's really not much different from the addition and subtraction that you do every day. The main thing to remember is to look for and combine like terms.
You can add two (or more) polynomials as you have added algebraic expressions. You can remove the parentheses and combine like terms.
Example | |||
Problem | Add. (3b + 5) + (2b + 4) | ||
(3b + 2b) + (5 + 4) | Regroup using the commutative property of addition and theassociative property of addition. | ||
5b + 9 | Combine like terms. | ||
Answer | (3b + 5) + (2b + 4) = 5b + 9 |
| |
Example | ||
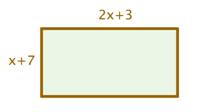
Problem | A rectangular garden has one side with a length of x + 7 and another with a length 2x + 3. Find the perimeter of the garden.
| |
(x + 7) + (2x + 3) + (x + 7) + (2x + 3) | The perimeter of a rectangle is the sum of its side lengths. | |
(x + 2x + x + 2x) + (7 + 3 + 7 + 3) | Regroup by like terms using commutative and associative properties. | |
6x + 20 |
Add like terms. | |
Answer |
The perimeter is 6x + 20. | |
The procedure is the same when you add polynomials that contain negative coefficients or subtraction:
Example | ||
Problem | Add. (-5x2 - 10x + 2) + (3x2 + 7x - 4) | |
-5x2 + (-10x) + 2 + 3x2 + 7x + (-4) | Rewrite subtraction as addition of the opposite. | |
(-5x2 + 3x2) + (-10x + 7x) + (2 - 4) | Regroup using commutative and associative properties. | |
-2x2 + (-3x) + (-2) |
Combine like terms. | |
Answer | (−5x2 - 10x + 2) + (3x2 + 7x - 4) = −2x2 - 3x - 2 | |
The above examples show addition of polynomials horizontally, by reading from left to right along the same line. Some people like to organize their work vertically instead, because they find it easier to be sure that they are combining like terms. The example below shows this "vertical” method of adding polynomials:
Example | ||||||||||||||||||||||||
Problem | Add. (3x2 + 2x - 7) + (7x2 - 4x + 8) |
| ||||||||||||||||||||||
| Write one polynomial below the other, making sure to line up like terms. | |||||||||||||||||||||||
| Combine like terms, paying close attention to the signs. | |||||||||||||||||||||||
Answer | (3x2 + 2x - 7) + (7x2 - 4x + 8) = 10x2 - 2x + 1 | |||||||||||||||||||||||
Sometimes in a vertical arrangement, you can line up every term beneath a like term, as in the example above. But sometimes it isn't so tidy. When there isn't a matching like term for every term, there will be empty places in the vertical arrangement.
Example | ||||||||||||||||||||||||||
Problem | Add. (4x3 + 5x2 - 6x + 2) + (−4x2 + 10) | |||||||||||||||||||||||||
| Write one polynomial below the other, lining up like terms vertically.
Leave a blank space above or below every term without a matching like term. | |||||||||||||||||||||||||
| Combine like terms, paying close attention to the signs. | |||||||||||||||||||||||||
Answer | (4x3 + 5x2 - 6x + 2) + (−4x2 + 10) = 4x3 + x2 - 6x + 12 | |||||||||||||||||||||||||
Find the sum. (4a2 + 5a + 7) + (8a + 2)
A) 9a2 + 8a + 9
B) 16a2 + 10a
C) 12a2 + 5a + 9
D) 4a2 + 13a + 9
|
When you subtract polynomials, you will add the opposite, as you have done with real numbers. So how do you find the opposite of a polynomial? Recall that the opposite of 3 is −3, and the opposite of −3 is 3. Just as the opposite of a number is found by multiplying the number by −1, we can find the opposite of a polynomial by multiplying it by −1.
Example | |||
Problem | Find the opposite of 9x2 + 10x + 5. | ||
(−1)(9x2 + 10x + 5) | Find the opposite by multiplying by−1. | ||
(−1)9x2 + (−1)10x + (−1)5
| Distribute −1 to each term in the polynomial. | ||
−9x2 + (-10x) + (−5)
| Multiply each coefficient by −1. | ||
Answer | The opposite of 9x2 + 10x + 5 is −9x2 - 10x - 5. | Rewrite addition of a negative term as subtraction. | |
Be careful when there are negative values or subtractions in the polynomial already.
Example | |||
Problem | Find the opposite of 3p2 - 5p + 7. | ||
(-1)(3p2 - 5p + 7) | Find the opposite by multiplying by -1. | ||
(-1)[3p2 + (-5)p + 7] | Change the subtraction to adding the opposite. | ||
(-1)3p2 + (-1)(-5)p + (-1)7
| Distribute -1 to each term in the polynomial and multiply each coefficient by -1. | ||
-3p2 + 5p + (-7) | Rewrite addition of a negative term as subtraction. | ||
Answer | The opposite of 3p2 - 5p + 7 is −3p2 + 5p - 7. | ||
Notice that in finding the opposite of a polynomial, you change the sign of each term in the polynomial.
Find the opposite of the polynomial. 8a3 - 3a - 2
A) -8a3 - 3a - 2
B) 8a3 + 3a - 2
C) 8a3 + 3a + 2
D) -8a3 + 3a + 2
|
Just as subtracting real numbers is the same as adding the opposite, you can subtract polynomials by adding the opposite of the second polynomial. Let's look at an example:
Example | |||
Problem | Subtract. (15x2 + 12x + 20) - (9x2 + 10x + 5) | ||
(15x2 + 12x + 20) + (-9x2 - 10x - 5) | Change the subtraction to adding the opposite. Be careful to change the sign ofeach term! | ||
(15x2 + -9x2) + (12x - 10x) + (20 - 5) | Regroup to match like terms. | ||
6x2 + 2x + 15 | Combine like terms. | ||
Answer | (15x2 + 12x + 20) - (9x2 + 10x + 5) = 6x2 + 2x + 15 | ||
When polynomials include a lot of terms, it can be easy to lose track of the signs. Be careful to transfer them correctly, especially when subtracting a negative term.
Example | ||
Problem | Subtract. (14x3 + 3x2 - 5x + 14) - (7x3 + 5x2 - 8x + 10) | |
(14x3 + 3x2 - 5x + 14) + (-7x3 - 5x2 + 8x - 10) | Rewrite as adding the opposite. | |
14x3 + 3x2 + (-5)x + 14 + (-7)x3 + (-5)x2 + 8x +(-10) | You may want to rewrite all subtractions as adding the opposite. | |
14x3 + (-7)x3 + 3x2 + (-5)x2 + (-5)x + 8x + 14 + (-10) | Regroup to put like terms together. | |
7x3 + (-2)x2 + 3x + 4 | Combine like terms. | |
Answer | (14x3 + 3x2 - 5x + 14) - (7x3 + 5x2 - 8x + 10) = 7x3 - 2x2 + 3x + 4 | |
Complex problems, like the one above, may be more easily solved using the vertical approach (shown below). However you choose to combine polynomials is up to you--the key point is to identify like terms, and be able to organize them accurately.
Example | |||||||||||||||||||||||||||||
Problem | Subtract. (14x3 + 3x2 - 5x + 14) - (7x3 + 5x2 - 8x + 10) | ||||||||||||||||||||||||||||
| Reorganizing using the vertical approach. | ||||||||||||||||||||||||||||
| Change the subtraction to adding the opposites, and combine like terms. | ||||||||||||||||||||||||||||
Answer | (14x3 + 3x2 - 5x + 14) - (7x3 + 5x2 - 8x + 10) = 7x3 - 2x2 + 3x + 4 | ||||||||||||||||||||||||||||
As with integer operations, experience and practice makes it easier to add and subtract polynomials.
Subtract. (4a3 - 5a + 7) - (8a3 - 3a - 2)
A) -4a3 - 8a + 5
B) --4a3 + 3a + 9
C) -4a3 - 2a + 9
D) -4a3 + 2a + 5
|
Summary
When adding or subtracting polynomials, use the commutative and associative properties to regroup the terms in a polynomial into groups of like terms. Change subtraction, including subtraction of the second polynomial, to addition of the opposite. When finding the opposite of a polynomial, be sure to change the sign of each term. Then you can combine the like terms.
Permissions
This reading is taken from the Developmental Math Open Program created by The NROC Project. It is available under a Creative Commons license.