Reading: Internal Rate of Return & Payback Period Analysis
Internal
Rate of Return (IRR)
- A project should only be accepted if its IRR is NOT less than the target internal rate of return. When comparing two or more mutually exclusive projects, the project having highest value of IRR should be accepted.
-NPV = 0; or
- PV of future cash flows − Initial Investment = 0; or

Find the IRR of an investment having initial cash outflow of $213,000. The cash inflows during the first, second, third and fourth years are expected to be $65,200, $96,000, $73,100 and $55,400 respectively.
Solution
Assume that r is 10%.
NPV at 10% discount rate = $18,372
Since NPV is greater than zero we have to increase discount rate, thus
NPV at 13% discount rate = $4,521
But it is still greater than zero we have to further increase the discount rate, thus
NPV at 14% discount rate = $204
NPV at 15% discount rate = ($3,975)
Since NPV is fairly close to zero at 14% value of r, therefore
IRR ≈ 14%
Payback
Period
- Accept the project only if its payback period is LESS than the target payback period.

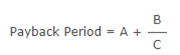
Example 1: Even Cash Flows
Company C is planning to undertake a project requiring initial investment of $105 million. The project is expected to generate $25 million per year for 7 years. Calculate the payback period of the project.
Solution
Payback
Period = Initial Investment ÷ Annual Cash Flow = $105M ÷ $25M = 4.2 years
Payback
Period Example
Example 2: Uneven Cash Flows
Company C is planning to undertake another project requiring initial investment of $50 million and is expected to generate $10 million in Year 1, $13 million in Year 2, $16 million in year 3, $19 million in Year 4 and $22 million in Year 5. Calculate the payback value of the project.

Payback Period
= 3 +
(|-$11M| ÷ $19M)
= 3 +
($11M ÷ $19M)
≈ 3 +
0.58
≈
3.58 years
