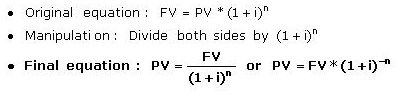In this video, we're going to discuss understanding present value. So, present  value is also called discounted value. It is the current worth of a future sum of  money or stream of cash flow, given a specified rate of return. Future cash flows are discounted at the discount rate, right? Or the interest rate. The higher the  discount rate, the lower the present value of the future cash flows, right?  Because the discount rate is going to be our cost of capital or the interest rate  that we are borrowing at, right. So, if we're going to discount future cash flows  and the interest rate, or the discount rate is higher, the stream of those future  cash flows on a present value basis will be lower. Determining the appropriate  discount rate is the key to properly valuing future cash flows, whether they are  earnings or obligations, right, obligations being debt obligations some kind of  payable. If you receive $10,000 today, the present value would be $10,000  because present value is what your investment gives you, if you were to spend it today, if you receive $10,000 in a year, the present value of that amount would  not be $10,000 because you do not have access to it now. It's not in your hand,  it's not in the present, right? So we can't spend it now. The present value is the  value of $1 what is worth today, so the future value of $1 we discount it back to  find the present value, right? So, if I have an income stream of $10,000 and I  receive that in five years, I want to know what that $10,000 is going to be worth  today, and is it worth me making that investment. To find the present value of the $10,000 you will receive in the future, you need to pretend the $10,000 is the  total future value of any amount that you invested today. In other words, to find  the present value of the future $10,000 we need to find out how much we would  have to invest today in order to receive that $10,000 in the future, so to figure  out the future value, to figure out to find how we are going to receive that  $10,000 at a certain discount rate. Right, we need to know, we want to find out  how much do we have to invest right now today at a certain rate, at a given rate, you know how much will we have to invest to receive the $10,000 that we need.  So to calculate present value, or the amount that we would have to invest today,  you must subtract the hypothetical accumulated interest from the 10,000 to  achieve this we can discount the future payment amount 10,000 by the interest  rate for the period. In essence, all you are doing is rearranging the future value  equation above so that you may solve for p. Okay, so or solve for present value,  the future, the above future value equation can be written, rewritten by replacing the p variable with the present value variable and manipulating the equation as  follows. Right, so for future value, so we have one plus our interest rate, n  stands for the number of periods that is going to be invested for, so let's just say  five with an interest rate of 10, right, 10% So now let's go over here to the board  real quick, so we can write this out, and then we can hypothetically take a look,  right. So we want to solve for future value. Okay, so we have the present value  right times one plus the interest rate raised to n, right, raised to the number of  periods, right. So let's say our present value is 1000 okay. Now multiply that. 

Let's say our interest rate is 10% right? And it's over five years. So now we're  going to do this simple math, right? 1.1 raised to the fifth. So now we have 1.1  raised to the fifth, right, so we do 1.1 right, and then we're going to raise that by  the exponent of five, right, that gives us 1.61051 right, and then we're going to  multiply that by 1000 okay, our present value, so times 1000 so the future value,  the future value of our $1,000 investment, right at our present value, we invest  1000 at 10% over five years, so that $1,000 invested at 10% over five years is  going to yield us $1,610.51 This is how we discover future value. Okay, now we  can find present value by manipulating the equation or changing it around just a  little bit, right. So we can go present value equals the future value over one plus  the interest rate raised by the number of periods. So let's say now our future  value is the 10,000 we discussed earlier, right. Okay, so we now in this equation  we're going to want to know the present value of our investment, and how much  are we going to have to invest over five years. Okay, that's our N, right, that's  our number of periods, five years. Okay, one plus our interest rate, we'll use the  same interest rate, 10% to keep it simple. Okay, so now we want to know, how  much do we have to invest today at 10% over the next five years? We want to  know how much we have to invest to receive $10,000 Okay, so first we'll want to do our exponent, right? So 1.1 raised to the fifth power, again it's 1.61051 right?  And we're going to divide that, so we're going to divide 10,000 by the 1.61051  so our present value to receive the $10,000 in five years at 10% we will have to  invest today at 10% over five years to receive 10,000 we will have to, we will  have to invest $6,209.21 so if we invest from today $6,209.21 at 10% interest  over five years, we will then receive the $10,000.



Last modified: Monday, July 6, 2026, 8:56 AM